材料的光学性能
仅供学习交流使用,内容来自2025年秋季学期。本人不对本文中的图片保有版权。
公式没渲染出来的话刷新一下网页就好了。
光与物质的作用
宏观上:透射、吸收、反射、散射
微观上:光子与固体中的原子、离子、电子之间相互作用
相互作用的方式:
- 电子极化
- 电磁波的分量之一是迅速变化的电场分量;
- 在可见光范围内,电场分量与传播过程中遇到的每一个原子都发生相互作用引起电子极化,即造成电子云与原子核的电荷中心发生相对位移;
- 所以,当光通过介质时,一部分能量被吸收,同时光速减小,后者导致折射。
- 电子能态转变
- 电磁波的吸收和发射包含电子从一种能态转变到另一种能态的过程;
- 材料的原子吸收了光子的能量之后可将较低能级上的电子激发到较高能级上去,电子发生的能级变化ΔE与电磁波频率有关:$\Delta E=h\nu_{21}$
- 受激电子不可能无限长时间地保持在激发状态,经过一个短时期后,它又会衰变回基态,同时发射出电磁波,即自发辐射。
介质与光的相互作用
折射、散射、吸收和色散都是光和物资的相互作用的结果。
折射
$$n=\frac{v_{\text{真空}}}{v_{\text{材料}}}$$
折射率永远大于1
斯奈尔定律
折射率和角度正弦值的乘积为定值,即
$$\frac{sin i_1}{sini_2}=\frac{n_2}{n_1}=n_{21}$$
$n_{21}$是材料2相对于材料1的相对折射率
影响n值的因素
离子半径
光在介质中的速度$v=\frac{c}{\varepsilon \mu}$,一般无机材料的磁导率为1,$n=\sqrt{\varepsilon}$介电常数$\varepsilon$反映了介质的极化,离子半径越大,介电常数越大,n也增大
2.结构
各向同性材料只有一个折射率,是均质介质
除立方晶系外的其他晶系都是非均质介质。光进入非均质介质后分为振动方向垂直速度不等的两个波。称为双折射。

两束光中有一束严格遵循折射定律,n为常数,称为常光(o光)$n_o=n_2/n_1$,另一束光的折射率随入射角的改变而变化,称为非常光(e光)。当光沿平行光轴的方向入射,不发生双折射。
密堆积程度越高,折射率越高
3. 内应力
压应力区n大,拉应力区n小
反射
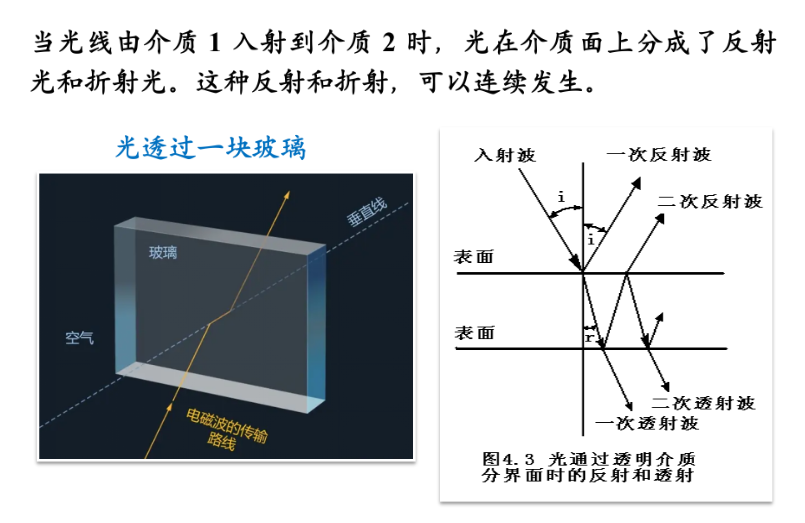
设光总能量流为$W=W’+W’’$,即入射光能量为反射光W’和折射光W’’的和。
反射系数m
$$m=\frac{W’}{W}=(\frac{n_{21}-1}{n_{21}+1})^2$$
投射系数$1-m$
两种介质的折射率越接近,反射损失越小。
eg:


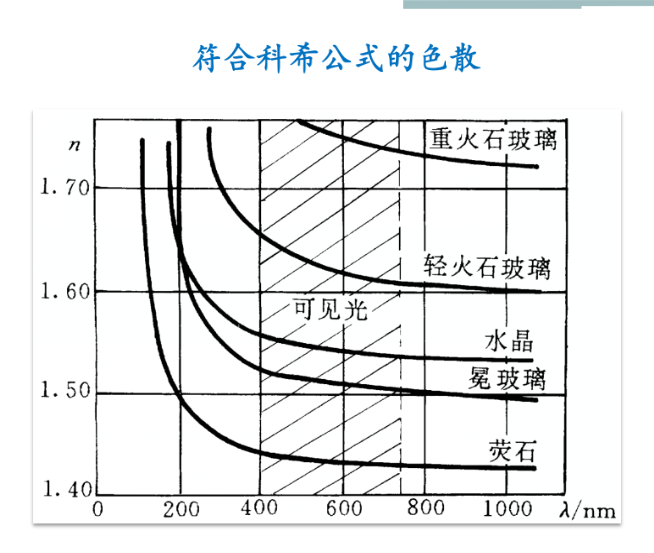
色散
材料的折射率与频率的线性关系称为折射率色散。$\mathrm{d}n/\mathrm{d}\lambda$
在普遍吸收波段内,物质表现出正常色散;
正常色散规律可以用科希公式来描述:
$$
n = A + \frac{B}{\lambda^2} + \frac{C}{\lambda^4}
$$
A、B和C是由物质性质决定的常量
若波长变化范围不大,科希公式可只取前两项,即:
$$
n = A + \frac{B}{\lambda^2}
$$
这时色散率可以表示为:
$$
\frac{dn}{d\lambda} = -\frac{2B}{\lambda^3}
$$
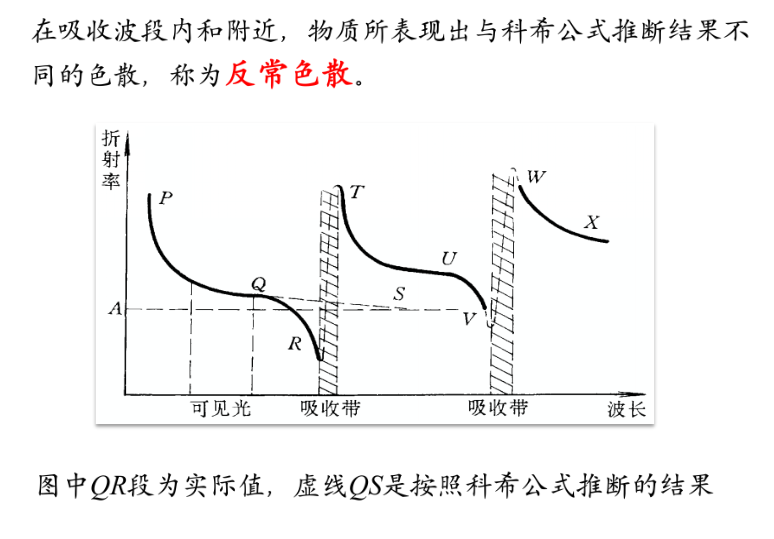
色散值的确定
阿贝数(色散系数),值越小色散越厉害。
$$\gamma=\frac{n_D-1}{n_F-n_C}$$
光纤的主要色散类型
材料色散
由于光纤的折射率随波长变化,使模式内不同波长的光时延不同产生的色散。波导色散
由于波导结构参数与波长有关产生的色散。
由于光纤的纤芯与包层折射率差很小,在交界面产生全反射时,可能有一部分光进入包层内,在包层内传输一定距离后,又可能回到纤芯中继续传输,这部分光相对于全反射光走过的距离长。模式色散(以阶跃型光纤为例)
不同入射角的光线,在光纤中的传播路径不同,但传播速度相同,到达输出端的时延不同,从而产生脉冲展宽,形成模式色散。
透光性与光吸收
一般规律
光强随厚度变化指数衰减,服从朗波特定律
$$I=I_0 e^{-ax}$$
a为光吸收系数,取决于材料性能和波长
吸收光谱
物质对光的吸收需要满足普朗克条件$h\nu=\Delta E$
气体吸收光谱
清晰狭窄的吸收线
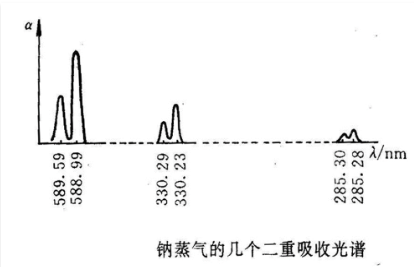
一般固、液吸收光谱
有一个宽的吸收带
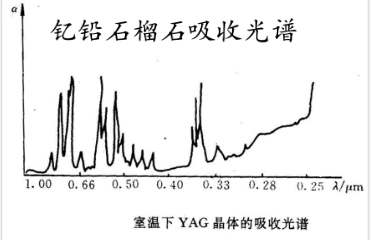
光吸收与光波长关系
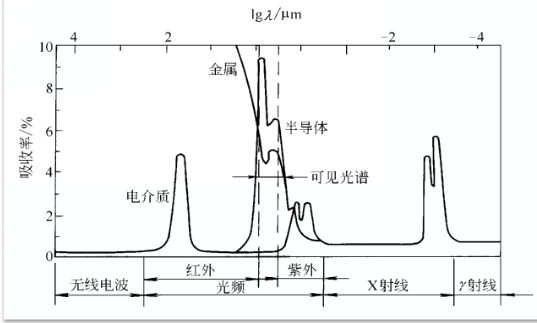
金属
金属材料对低频电磁波不透明,对高频电磁波透明。因为金属电子可以被可见光等激发到费米能级以上,所以金属不透明。
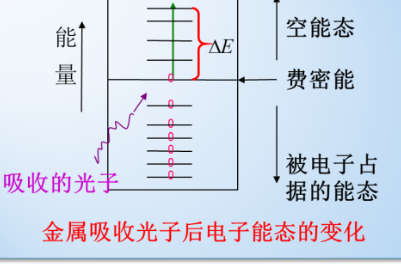
金属激发后释放光子回到基态,表现为反射光,金属的m通常在0.9左右
半导体
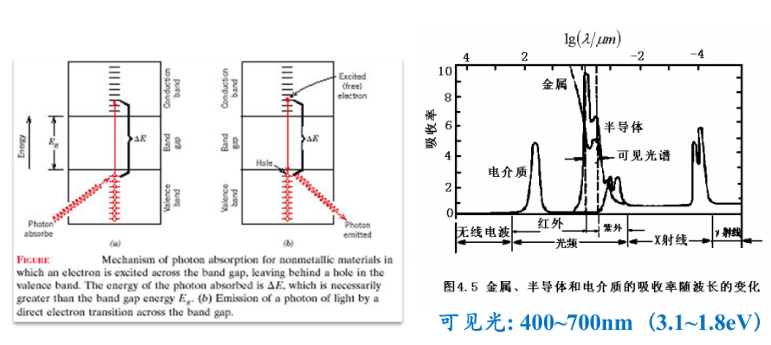
半导体的紧带不是很宽,电子容易跃迁到导带
电介质
禁带很宽,存在一个紫外吸收峰,红外吸收峰是离子的弹性振动和光子辐射谐振引起的
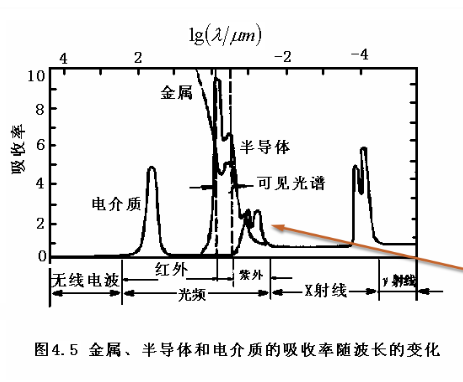
对于红外吸收峰
$$\gamma^2=2\beta(\frac{1}{M_c}+\frac{1}{M_a})$$
$\beta$ 为微观弹性模量,M为离子质量
为了获得较宽透明范围。需要尽可能小的热振频率和尽可能大的能隙。
- 可见光中波长最短的是紫光($\lambda_{\text{min}}=0.4,\mu\text{m}$),对应最大禁带能量:
$$
(E_{\text{g}}){\text{max}}=\frac{hC}{\lambda{\text{min}}}=3.1,\text{eV}
$$ - 可见光中波长最长的是红光($\lambda_{\text{max}}=0.7,\mu\text{m}$),对应最小禁带能量:
$$
(E_{\text{g}}){\text{min}}=\frac{hC}{\lambda{\text{max}}}=1.8,\text{eV}
$$
$E_{\text{g}} < 1.8,\text{eV}$(半导体材料)
- 光学特性:不透明
- 原因:所有可见光的能量都足以激发价带电子跃迁到导带,因此会被完全吸收。
2. $E_{\text{g}} = 1.8,\text{eV} \sim 3.1,\text{eV}$(非金属材料)
- 光学特性:带色透明
- 原因:只有能量大于禁带宽度的部分可见光会被吸收,其余波长的光可以透过,因此呈现特定颜色。
3. $E_{\text{g}} > 3.1,\text{eV}$(非金属材料)
- 光学特性:无色透明(不考虑反射和散射)
- 原因:可见光的能量不足以跨越禁带,无法激发电子跃迁,因此不会被吸收。
散射
光通过介质时遇到烟尘等杂质偏离原传播方向,向各个方向弥散。
原因:光遇到不均匀结构产生次级波,与主波合成产生干涉现象,使得光偏离原方向发生散射。
散射和吸收一样使光强减弱,对于相分布均质材料,有$I=I_0\exp{[-(a+S)x]}$,
S为散射系数,a为吸收系数。
质点尺寸约等于入射波长$\lambda$时散射最强
散射分为
- 弹性散射,散射光波长不变
- 非弹性散射,散射光波长改变
菲涅尔散射
认为反射和折射引起的总体散射起到主导作用
基体与散射质点的折射率差异 $\to$ 连续的反射和折射
$$S=\frac{3KV}{4R} $$
瑞利散射
光在尺度小于波长的微粒上发生的弹性散射。
当$d<0.1\lambda$时,近似有瑞利散射公式散射光的强度与波长的四次方成反比
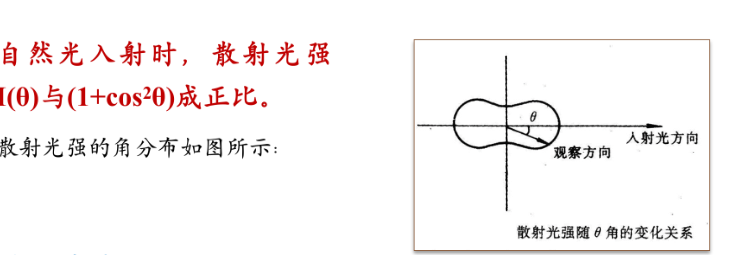
不均匀介质如乳状液的瑞利散射是悬浮质点散射,均匀介质如气体中的瑞利散射是分子散射。
米氏散射
当散射粒子的尺度相当于波长,为大粒子散射,称为米氏散射。
$$a<\frac{0.3\lambda}{2\pi}$$
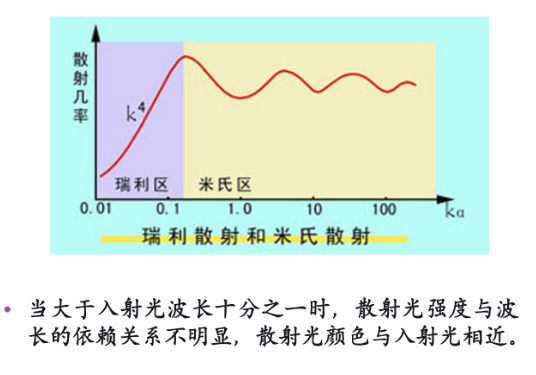
决定散射系数的主要因素包括第二相颗粒尺寸、颗粒体积含量、相对折射率等
拉曼散射
拉曼散射是一种非弹性散射,使得散射光的波长改变。
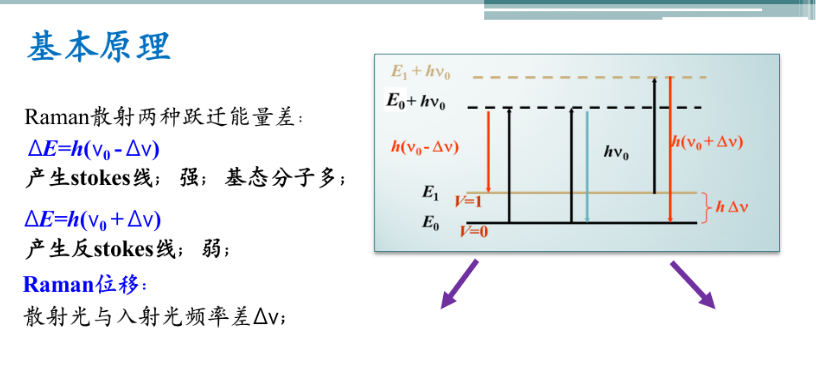
拉曼散射的特征
每条原始入射谱线两旁都伴有频率差 $\omega_j$($j=1,2,3,\dots$)相等的散射谱线。
- 这些散射谱线称为拉曼谱线,分布在入射光两侧。
- 频率差 $\omega_j$ 对应于分子振动或转动能级之间的跃迁。
频率差 $\omega_j$ 与入射光的频率无关,表征了散射物质的分子振动频率。
- 说明拉曼位移仅由材料本身的结构决定,是物质的“指纹”。
- 可用于识别物质的化学组成和分子结构。
拉曼效应来自于入射光子和分子振动能级的能量交换。
拉曼光谱是重要的物质分析手段。
拉曼散射过程详解
1. 激光选择原则
测定拉曼散射光谱时,一般选择激发光能量满足以下条件:
- 大于分子振动能级的能量(以实现非弹性散射)
- 低于电子能级间隙(避免激发电子跃迁)
- 远离分析物的紫外-可见吸收峰(防止荧光干扰)
目的:确保主要发生拉曼散射而非荧光或电子跃迁。
2. 能量变化过程
光与样品分子作用时,分子被激发至一个能量较高的虚态。
左边一组线代表分子与光作用后的能量变化,粗线表示出现的概率大小。
- 分子从基态吸收光子进入虚态;
- 然后跃迁到不同振动能级并发射散射光子;
- 散射光频率发生变化,形成拉曼位移。
3. 散射强度分布(室温下)
在室温下,处于基态最低振动能级的分子数目最多,因此:
- 与光子作用后返回同一振动能级的概率最大 → 瑞利散射最强
- 返回较低振动能级 → 发出 Stokes 线(频率降低)
- 返回较高振动能级 → 发出 反 Stokes 线(频率升高)
散射几率大小关系为:
瑞利散射 > Stokes 线 > 反 Stokes 线
4. 物理意义
- Stokes 线:分子从基态跃迁到激发态,同时释放多余能量 → 更常见
- 反 Stokes 线:分子已处于激发态,吸收光子后跃迁回更低能级 → 数量少,信号弱
- 因此,在实验中通常以 Stokes 线为主进行分析。
影响材料透光率的因素
透光率是指光线通过材料时,透射光强与入射光强之比。影响材料透光率的主要因素包括吸收、反射和散射。其透射光强可由以下公式描述:
$$
I = I_0 (1 - m)^2 e^{-(\alpha + S)x}
$$
其中:
- $I_0$:入射光强度
- $I$:透射光强度
- $m$:表面反射损失系数(通常为反射率)
- $\alpha$:吸收系数
- $S$:散射系数
- $x$:材料厚度
1. 吸收系数 $\alpha$
陶瓷、玻璃等电介质材料在可见光范围内吸收率较低,光吸收损失相对较小,在影响透光率的因素中不占主导地位。
特点:
- 对于透明材料(如石英玻璃),$\alpha$ 很小,可忽略;
- 但若材料中含有过渡金属离子或缺陷,会显著增加吸收。
2. 反射系数
材料对周围环境的相对折射率越大,反射损失也越大;同时,材料表面的光洁度直接影响透光性能。
原理:
光从空气进入材料界面时发生反射,反射率 $R$ 由菲涅尔公式决定:
$$
R = \left( \frac{n_1 - n_2}{n_1 + n_2} \right)^2
$$
其中 $n_1, n_2$ 分别为空气和材料的折射率。
改善方法:
- 表面抛光以减少粗糙度;
- 使用抗反射涂层(AR coating)降低界面反射。
3. 散射系数 $S$ —— 对陶瓷材料透光率的影响最大
散射是导致多晶陶瓷透光性差的主要原因,尤其在微观结构不均匀的情况下更为显著。
① 材料宏观及显微缺陷
| 缺陷类型 | 影响机制 |
|---|---|
| 夹杂物、掺杂、晶界 | 折射率与主晶相不同 → 在不均匀界面上形成相对折射率 |
📌 相对折射率越大 → 界面处反射系数越大 → 散射系数 $S$ 越大 → 透光率下降
② 晶粒排列方向
多晶材料中存在双折射现象,晶粒之间因取向不同而产生折射率差异。
过程说明:
- 光线穿过左晶粒时沿某一方向传播;
- 到达右晶粒时,由于晶轴方向改变,e光的折射率发生变化;
- 导致在晶界处出现相对折射率 $n_o/n_e \neq 1$;
- 引起晶界处的反射和散射损失。
总结:提高陶瓷材料透光性的关键措施
| 措施 | 作用机制 |
|---|---|
| 减少杂质和夹杂物 | 降低异相引起的相对折射率 |
| 控制晶粒尺寸与分布 | 减少晶界数量和不均匀性 |
| 提高烧结密度 | 减少孔隙,增强连续性 |
| 优化晶粒取向 | 减少双折射效应 |
| 表面处理与镀膜 | 降低表面反射损失 |
实际应用中,透明陶瓷(如氧化铝、氧化钇)需通过高纯原料、热压烧结、晶粒定向控制等手段实现高透光率。