材料的导电性能
仅供学习交流使用,内容来自2025年秋季学期。本人不对本文中的图片保有版权。
公式没渲染出来的话刷新一下网页就好了。
电导性能的核心在于
$$\sigma=\sum_i \sigma_i=\sum_i n_i q_i \mu_i$$
电导现象
电导的宏观参数
电导率和电阻率
$$I=\frac{V}{R}$$
$$R=\rho\frac{L}{S}$$
电阻率
$$\rho=R\frac{L}{S}$$
电阻率是材料的本征参数,单位为$\omega\cdot m$
绝对零度下,载流子像理想气体一样自由运动,迁移率无穷大。当原子因热运动偏离平衡或缺陷破坏了对称性,电子偏离了周期性势场而受到散射,这就是经典理论中电阻的来源。
$$\rho=\rho_L+\rho_R$$
$\rho_L$是晶格振动散射的电阻率,与温度有关;$\rho_R$是受杂质影响的电阻率,与温度无关,绝对零度下也存在,称为剩余电阻。
定义电导率
$$\sigma=\frac{1}{\rho}(S/m)$$
欧姆定律可以用电流密度J表示,$J=\sigma E$(微分形式)
体积电阻和表面电阻
电流由体积电流和表面电流组成$I=I_V+I_S$
总电阻
$$\frac{1}{R}=\frac{1}{R_V}+\frac{1}{R_S}$$
等效为一并联电路
电导的物理特性
带电荷的自由粒子称为载流子。
电流密度$J=\sigma E=nqv$
定义迁移率
$$\mu=\frac{v}{E}$$
则电导率$\sigma=nq\mu$
$$\sigma=\sum_i \sigma_i=\sum_i n_i q_i \mu_i$$
霍尔效应
载流长方体薄板上沿电流的垂直方向施加磁场,则在与电场、磁场都垂直的方向出现电势差。
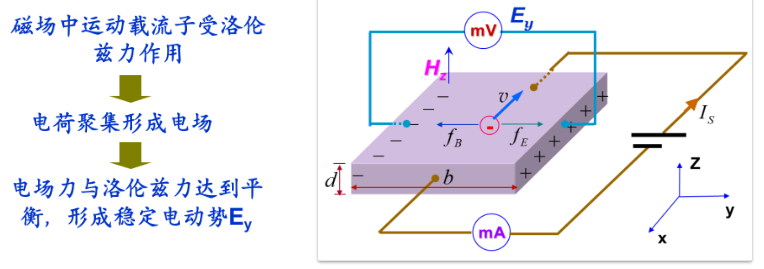
霍尔电压$U_H=R_H\frac{IB}{d}$,$R_H$是霍尔系数,为一本征参数
推导有
$$R_H=\frac{1}{\pm ne}$$
正负号与载流子符号一致
霍尔迁移率$\mu_H=R_H\sigma$
离子电导
- 本征电导,点阵上基本离子的运动,高温下显著
- 杂质电导,固定较弱的离子的运动,低温下显著
离子半径小、电价低的离子,在晶体中键型主要是离子键,易迁移。
扩散机制分类(离子扩散)
在离子导电材料中,载流子的迁移方式主要分为以下三种扩散机制:
1. 空位扩散
- 定义:金属离子留下的空位作为载流子的扩散运动。
- 特点:
- 载流子通过占据相邻空位实现移动;
- 是最常见的扩散机制之一;
- 通常发生在具有缺陷结构的晶体中。
代表:如金属中的原子空位扩散。
2. 间隙扩散
- 定义:间隙离子作为载流子,从一个间隙位置直接扩散到另一个间隙位置。
- 特点:
- 不依赖于空位,而是利用晶格中的间隙空间;
- 一般比空位扩散需要更高的能量;
- 较难进行,常见于小尺寸离子(如 $H^+$、$Li^+$)。
注意:由于能垒较高,该机制在多数情况下不占主导。
3. 亚晶格间隙扩散
- 定义:某一间隙离子取代附近晶格离子,被取代离子进入晶格间隙,从而产生移动。
- 特点:
- 由晶格变形引起,因此较容易发生;
- 涉及晶格结构的局部重构;
- 与晶格畸变密切相关。
典型例子:AgBr 中的银离子($Ag^+$)就是通过这种机制进行扩散。
载流子浓度
固有电导
固有电导是晶体本身的热缺陷提供的载流子
弗伦克尔缺陷
晶格振动时一些质点离开平衡位置进入间隙,在原来的位置形成空位,形成一对载流子。
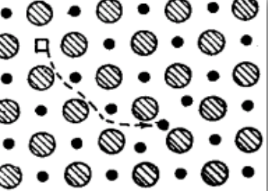
生成相同浓度的间隙离子和空位
$$N_f=N \exp \frac{-E_f}{2kT}$$
肖特基缺陷
格点跃迁到晶体表面而在原来的地方留下一个空位
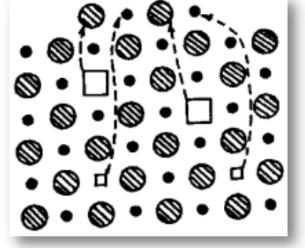
出现正离子空位和负离子空位,伴随晶体体积增加
$$N_s=N \exp\frac{-E_s}{2kT}$$
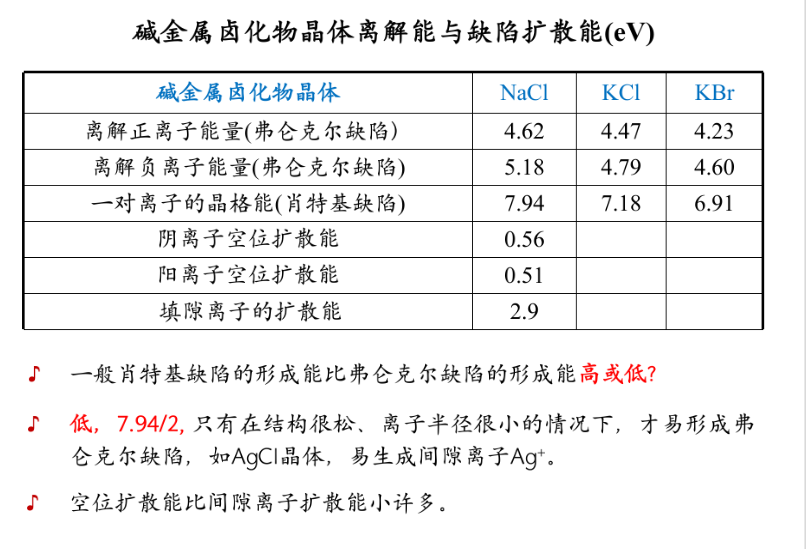
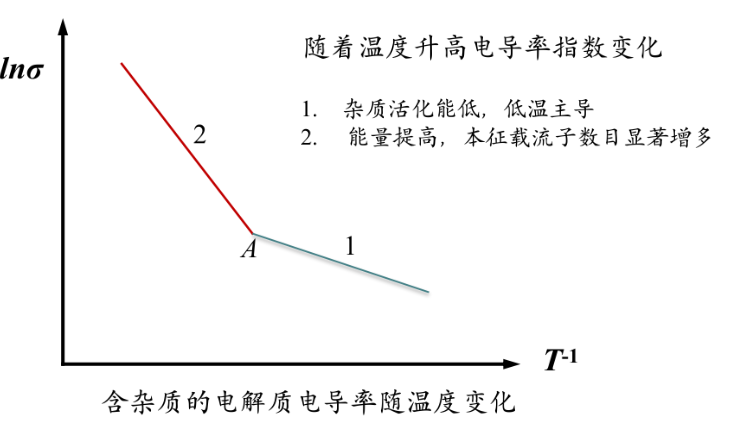
杂质电导
杂质的迁移活化能远低于晶体热缺陷活化能,离子晶体的电导主要是杂质电导
离子电导率与扩散系数的关系$\sigma=D\frac{nq^2}{kT}$
影响离子电导的因素
- 温度
晶体结构
- 熔点
- 电荷
- 间隙大小
晶格缺陷 不等价离子掺杂等
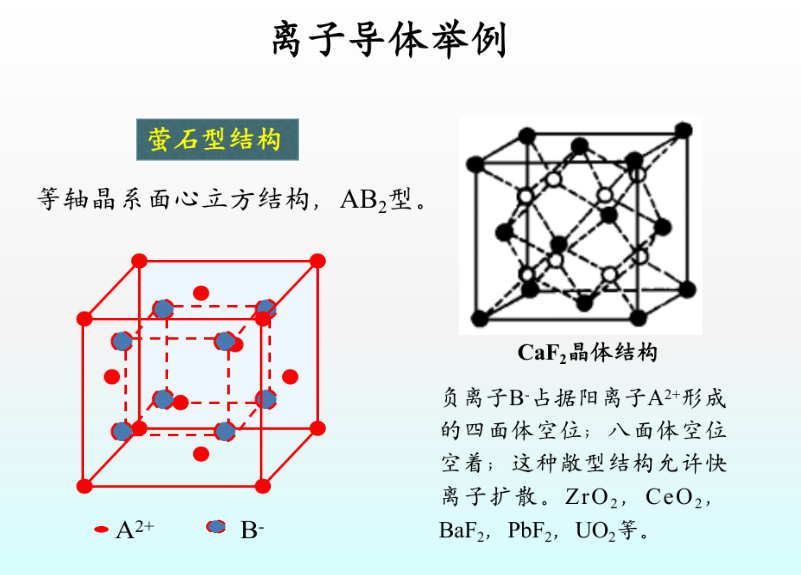
固体电解质
离子晶体具有离子电导,称为固态电解质 ,如萤石
电子电导
载流子是电子或空穴,发生在金属或半导体中。
电子电导的电阻率来自于散射
对于金属,电子散射来自于杂质、缺陷、声子等。
对于半导体,载流子散射的来源有
- 电离杂质散射
- 声子散射
- 中性杂质散射
- 位错散射
- 载流子散射
电子迁移率
金属的电子近似为自由的,其在电场作用下按照经典理论被电场力加速,并受到声子等阻碍,其迁移率为
$$\mu=\tau\frac{e}{m_e}$$
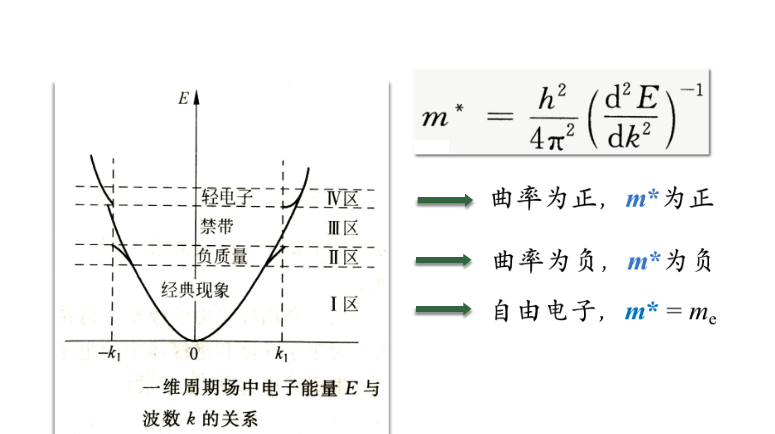
半导体的电子不自由,能量量子化,其有效质量
$$m^=\frac{h^2}{4\pi^2}(\frac{\mathrm{d^2}E}{\mathrm{d^2}k})$$
晶格场中电子迁移率
$$\mu=\tau\frac{e}{m^}$$
有效质量包括了晶体与电子的相互作用
载流子浓度
晶体中只有导带电子和价带顶部空穴才能导电
金属
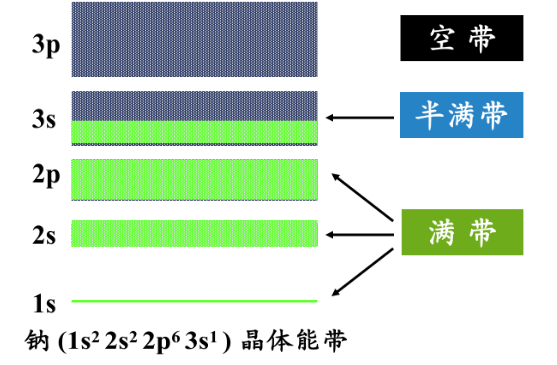
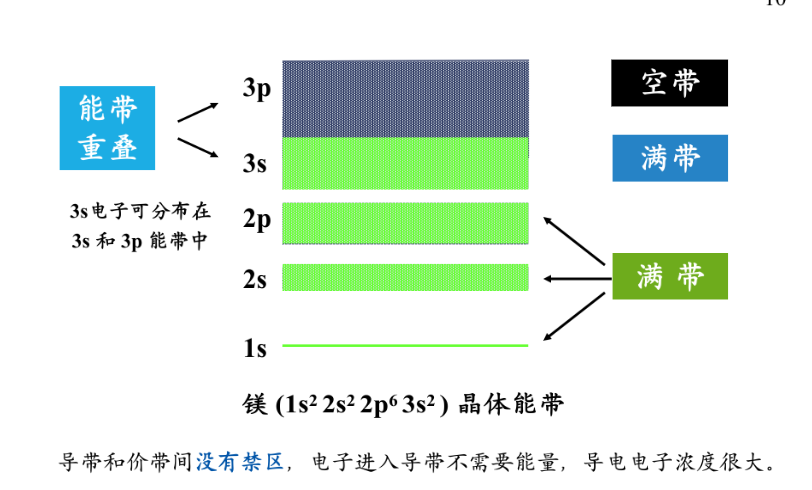
半导体

绝缘体

本征半导体
在外界作用下,价带电子获得能量,跃迁到导带,导带出现导电电子,价带留下空穴。
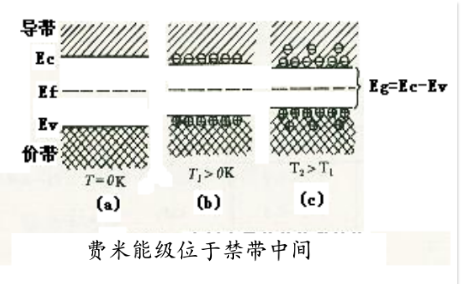
杂质半导体
- n型半导体的载流子为电子
- p型半导体的载流子为空穴
掺杂方式包括间隙式杂质和替换式杂质
施主杂质 多余价电子的杂质,仅需很小能量(Si-P 体系的杂质电离能0.044eV)就能产生导电电子
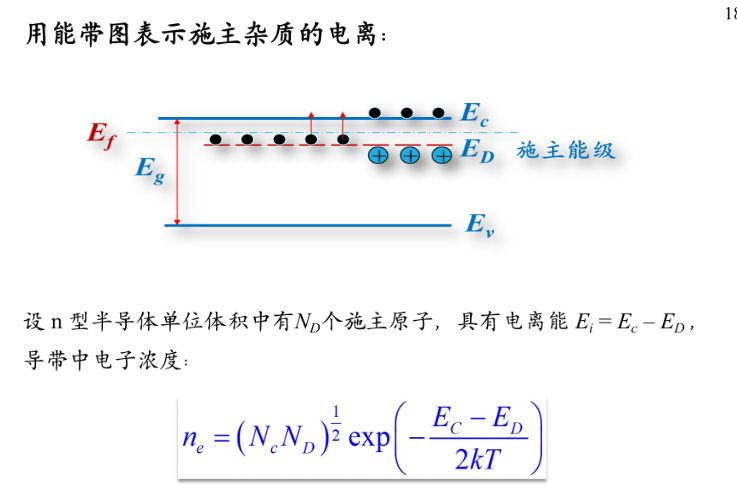
受主杂质 多余空穴引入
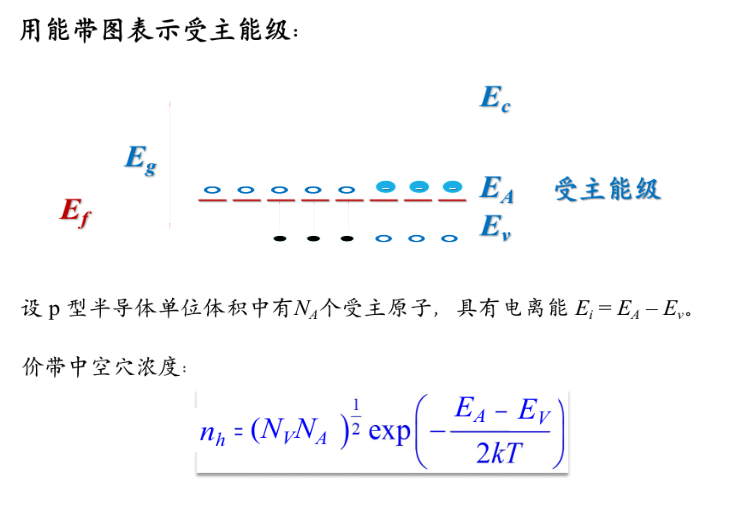
载流子浓度符合对温度的指数分布规律
影响电导率的因素
温度
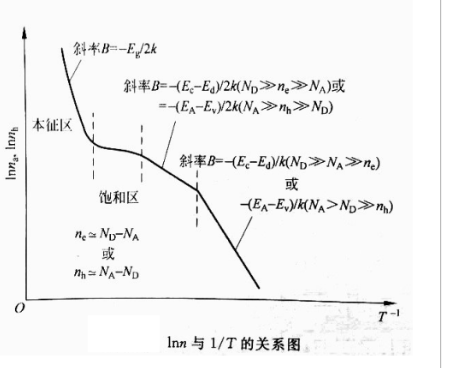
杂质
组分缺陷
阳离子空位缺陷是受主能级 ,阴离子空位缺陷是施主能级
半导体陶瓷的物理效应
表面效应
表面能级
自由表面使得周期势场中断,引入表面能级
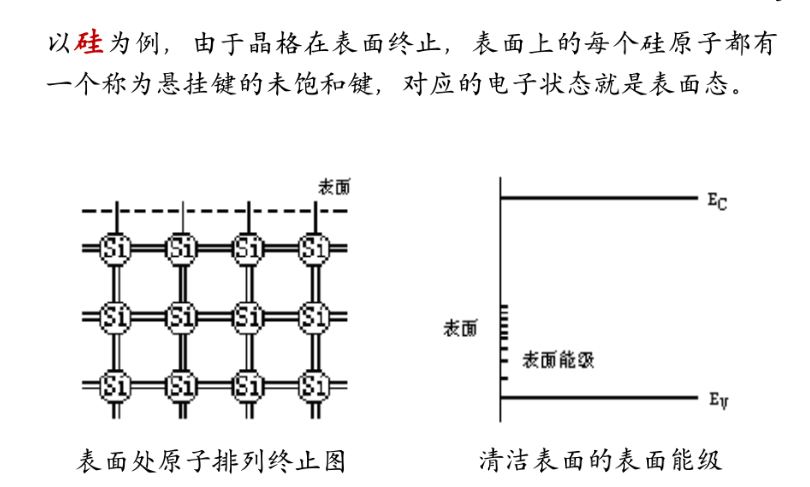
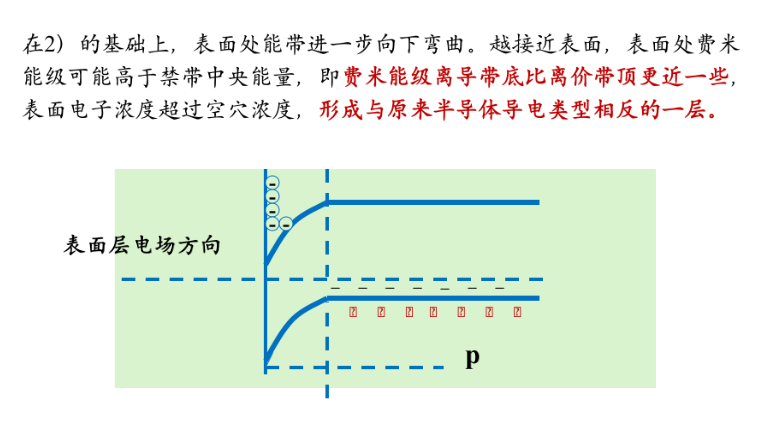
以p型半导体为例
- 多数载流子堆积状态
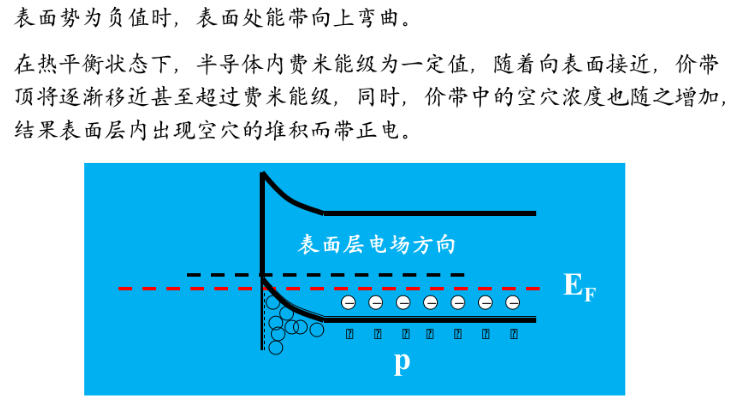
- 多数载流子耗尽
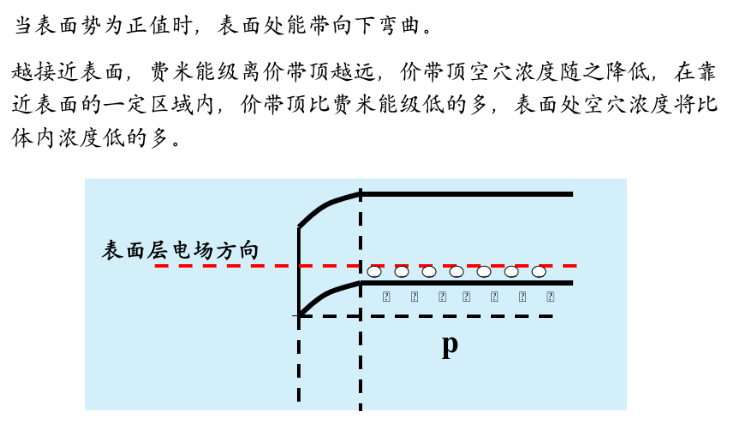
- 少数载流子反型,形成与原来半导体导电类型相反的类型
表面效应(吸附)
吸附气体电导率发生变化的现象
如果气体的电子亲和能大于半导体功函数,则吸附分子得到电子带负电,称为负电吸附;反之为正电吸附。
表面形成耗尽层,电导率会减小;形成载流子累计区则表面电导率增加
- 一般氧化气体易造成负电吸附,还原气体引起正电吸附。
- 温度也会影响吸附离子的形态
气敏半导体
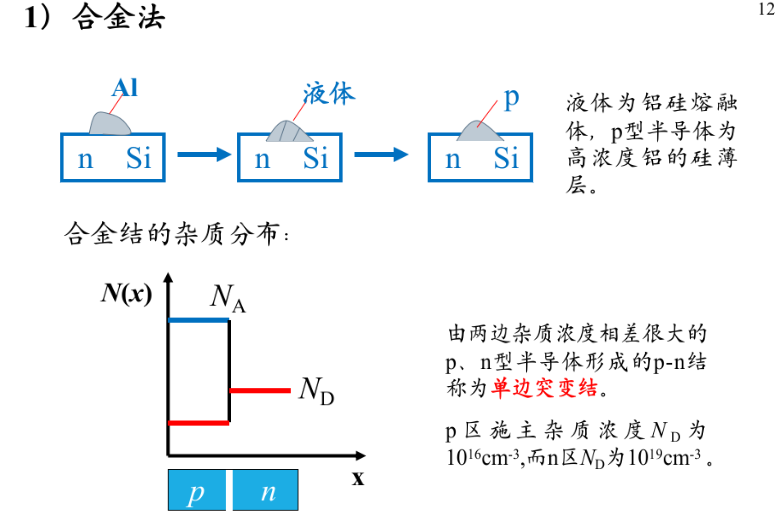
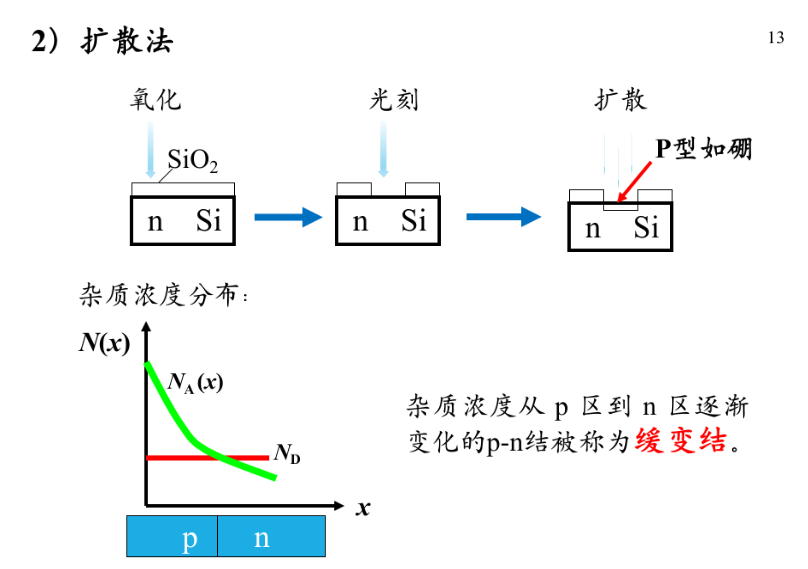
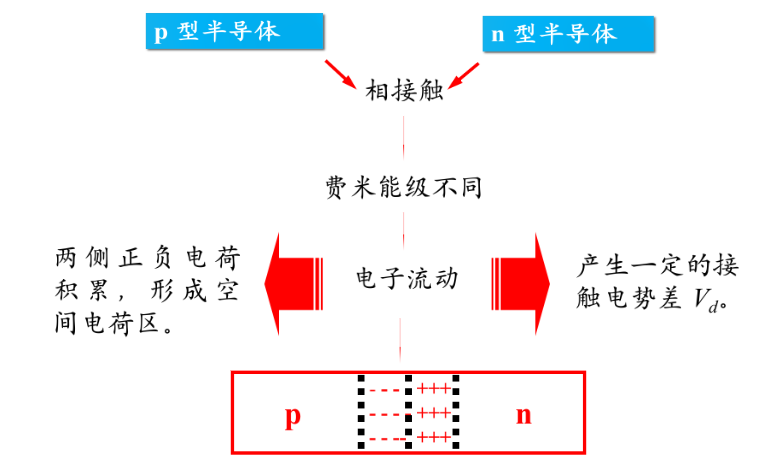
p-n结
西贝克效应
金属、半导体温差电动势
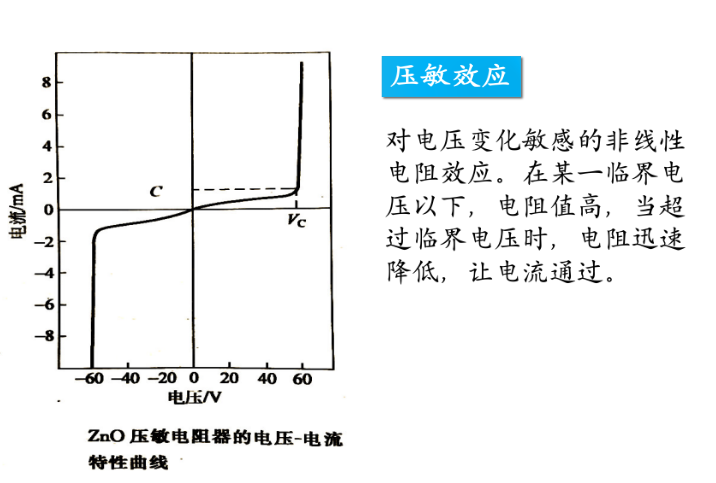
压敏效应
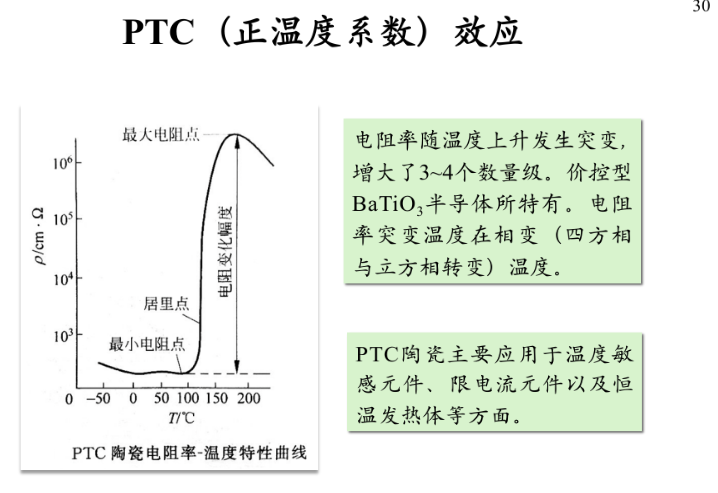
PTC相变正温度系数效应
p-n结接触空间电荷取的电势能从n$\to$p区升高,势垒高度 $qV_d=E_{F_n}-E_{F_p}$.
金属与半导体接触有
- 肖特基接触
- 欧姆接触
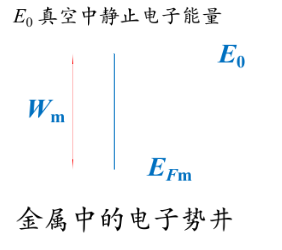
金属的功函数$W_m=E_0-(E_F)_m$
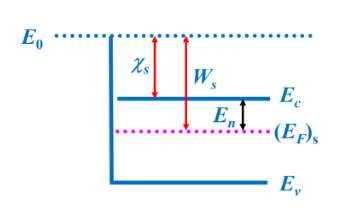
半导体的功函数$W_s=E_0-(E_F)_s=\chi_s+E_n$,$E_n$为导带底与费米能级的差,$\chi_s$为电子亲和能
整流接触
当金属与n型半导体接触,且金属的功函数大于半导体形成一个半导体指向金属的电场,产生一个势垒,作为高阻层
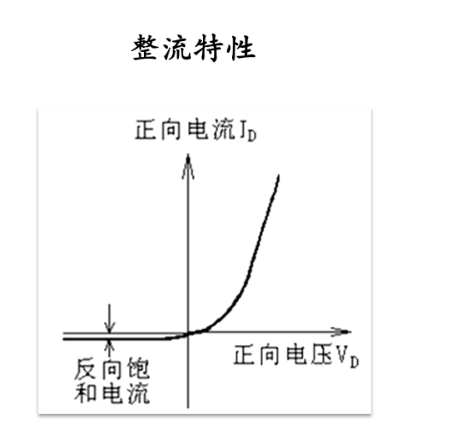
反正,形成一个积累层,双向导通
非整流接触
不产生附加电阻,符合欧姆定律
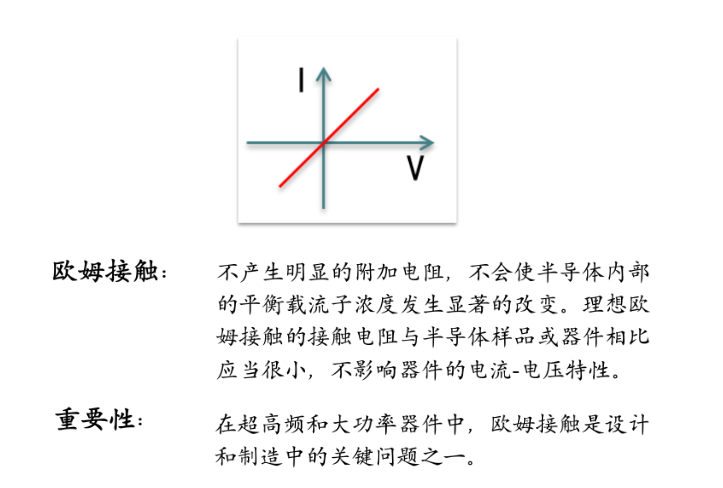

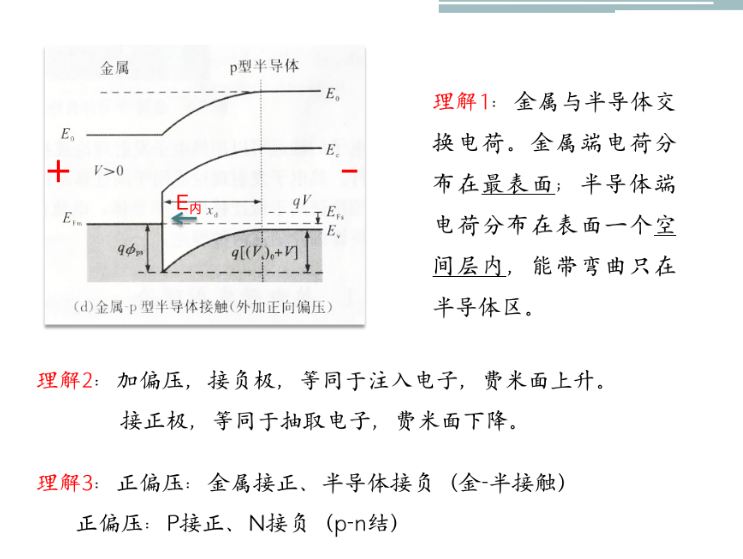
当金属与半导体间形成阻挡层时称为肖特基基础,肖特基势垒高度是肖特基接触的唯一重要参数
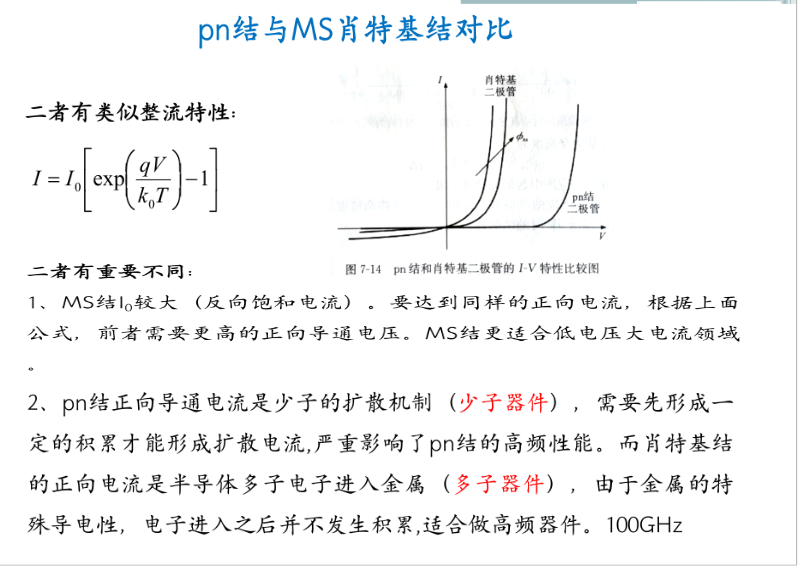
肖特基器件更适合在高频下工作