材料的热性能

---

仅供学习交流使用，内容来自2025年秋季学期。本人不对本文中的图片保有版权。

公式没渲染出来的话刷新一下网页就好了。

---

热的物理本质

材料的热性能来自于其晶格的热振动，晶格中各质点的热运动动能总和就是该物体的热量。

考虑一维简单晶格，将质点的运动方程近似为简谐振动方程
$$m\frac{\mathrm{d}x_n^2}{\mathrm{d}t^2}=\beta(x_{n+1}+x_{n-1}-2x_n)$$
其中$\beta$为微观弹性模量。

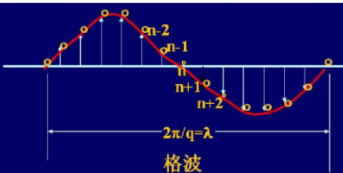
质点间存在相互作用，一个质点的振动会带动其他质点，相邻质点间的振动存在相位差，使得晶格振动以弹性波形式在材料内传播。

考虑一维双原子链的复格子，其振动方程的解有平面波的形式

其中存在两种不同的色散关系，即存在两种独立的格波。

• 声学波
• 光学波

声学支的长波极限 振幅$\frac{B}{A}\to 1$,两种原子的振幅和相位趋于一致，运动方式没有差别。长声学波代表原胞质心整体的移动。

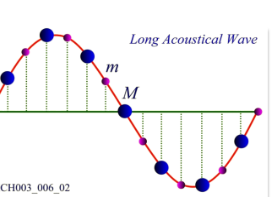
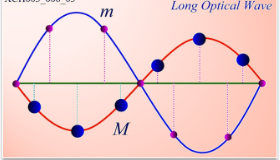
光学支的长波极限 振幅$\frac{B}{A}=-\frac{m}{M}$

同种原子振动相位一致，相邻原子振动相反。长光学波代表原胞质心不动的振动，不同原子做相对振动。

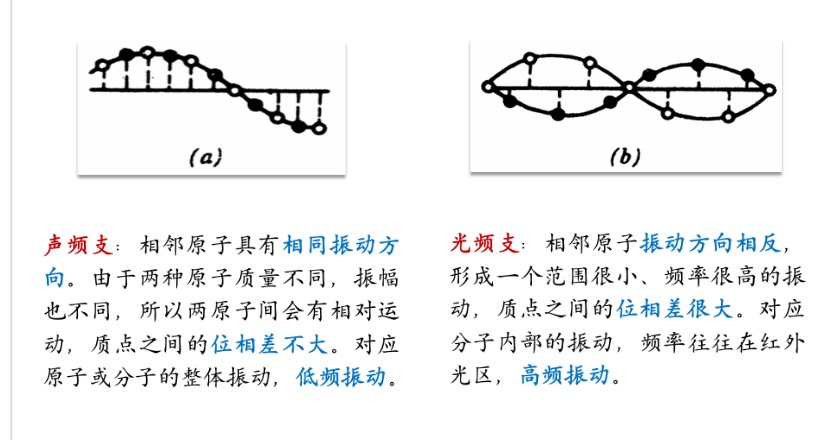
弹性波声频支的最大频率约为$1.5\times10^{13}Hz$

一维双原子链中，一个分子（化学计量数比）中有n个不同原子，则有n-1个光频波；晶格中有N个分子，则有N(n-1)个光频波。三维体系中均$\times 3$

格波能量的量子化

• 振动微弱时格波可近似为简谐波
• 简谐波间相互作用被忽略，相互独立
• 晶体的周期性边界条件（玻恩-卡门），使得独立的振动态分立

$\to$ 格波能量可量子化，$E_n=(n+\frac{1}{2})\hbar\omega$

三维晶格振动总能量为
$$E=\sum_{i=1}^{3nN}(n_i+\frac{1}{2}\hbar\bar{\omega_i)}$$
$\hbar\omega_i$称为声子，反应晶格原子的集体运动状态。

热容

热容包括晶格热容和电子热容两部分。一般以前者占主导。
$$C=(\frac{\partial Q}{\partial T})_T$$
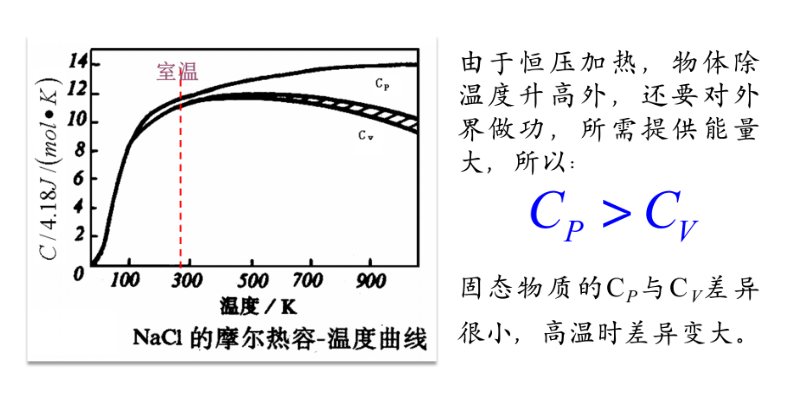
恒压热容
$$C_P=(\frac{\partial Q}{\partial T})_P=(\frac{\partial H}{\partial T})_P$$
恒容热容
$$C_V=(\frac{\partial Q}{\partial T})_V=(\frac{\partial E}{\partial T})_V$$

---

热容理论

杜隆-柏替定律

室温恒压下几乎所有单原子固体摩尔热容为$C_P=25J\cdot mol^{-1}\cdot K^{-1}$，
轻原子略低于该值。

柯普定律

化合物的分子热容等于各元素原子热容和
$$C=\sum n_ic_i$$
这两条定律是从经典理论能量均分原理推出的自然结果，在高温下结果较好。

量子理论的引入

低温下热容按$T^3$律减小，需要量子理论的解释。

质点的能量只能取能量量子的整数倍，直接求解$C_V$是困难的，实际采用简化的爱因斯坦和德拜模型

爱因斯坦模型

假设谐振子相互独立，以相同角频率振动
$$\bar E =3N \frac{\hbar\omega}{\exp{(\frac{\hbar \omega}{kT})}-1}$$
$$C_V=(\frac{\partial E}{\partial T})_V=3Nkf_e{\frac{\hbar \omega}{kT}}$$
定义爱因斯坦温度$\Theta_E=\frac{\hbar \omega}{k}$

高温时，$C_V\to3Nk=3R$,与杜隆-柏替定律一致

低温时，$C_V=3Nk(\frac{\Theta_E}{T})^2\exp{(-\frac{\Theta_E}{T})}$,与实际T3律不符。这说明原子间振动不独立，爱因斯坦模型过于简化。

德拜模型

将晶体视为连续介质，因此有连续的弹性波。声频支也是连续的，频率从$0\sim \omega_{max}$

仿照爱因斯坦模型，有

热容
$$C_V=3NKf_D(\frac{\Theta_D}{T})$$
特征温度
$$\Theta_D=\frac{\hbar\omega_{max}}{k}$$

德拜模型在低温下$C_V=\frac{12\pi ^4Nk}{5}(\frac{T}{\Theta_D})^3$,与实验值吻合非常好

德拜温度——晶体具有的固定特征值。

• 当 $T < \Theta_D$ 时，只能激发出较低频声子，且声子数目也随着温度减少，即长波（低频）主要。
• 当 $T > \Theta_D$ 时，能量最大的声子被激发出来，即德拜温度是最大能量声子被激发出来的温度。
• 在 $T >> \Theta_D$ 时，声子的数目与温度成正比，频率不变。

德拜温度也能用经验公式求得
$$
\Theta_D = 137 \sqrt{\frac{T_m}{M V_a^{2/3}}}
$$
可见熔点高-原子间结合力强-$\Theta_D$高，所以$\Theta_D$为选用高温材料考虑的因素之一。

德拜模型对原子晶体拟合很好，但是对于金属，其电子热容不能忽略，金属的低温热容正比于T.

温度变化，在宏观上表示放热吸热，实质是各频率的声子分布发生变化。

实际材料的热容

影响因素

1. 温度
2. 结构（气孔率等）
3. 相变

固溶体、化合物和多相复合材料的热容近似满足柯普定律。

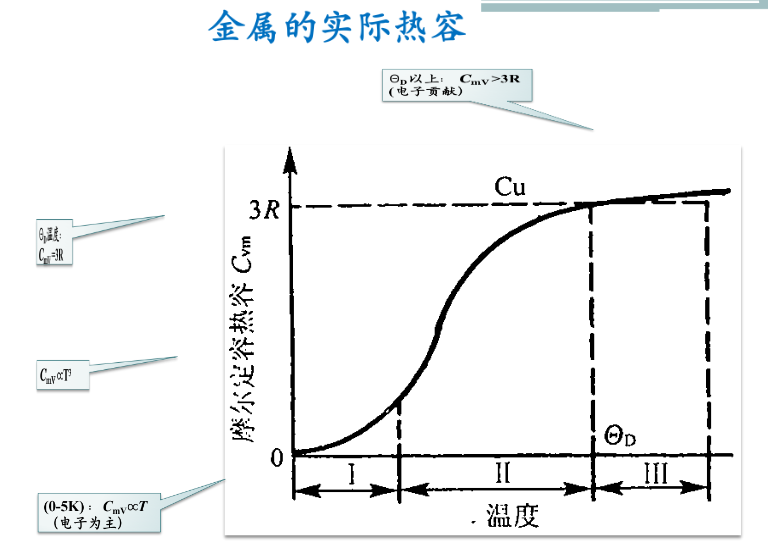
金属在低温下必须考虑自由电子对热容的贡献
$C_{mV}=C_{mV}^p+C_{mV}^e=bT^3+\gamma T$

热膨胀

$$\frac{\Delta l}{l_0}=a_l \Delta T$$
$a_l$为线膨胀系数，通常随温度升高增大。

体膨胀系数为三方向线膨胀系数的和。

热膨胀机理

简谐振动的平衡位置不会随着振幅增大改变，因此热膨胀是非线性效应。

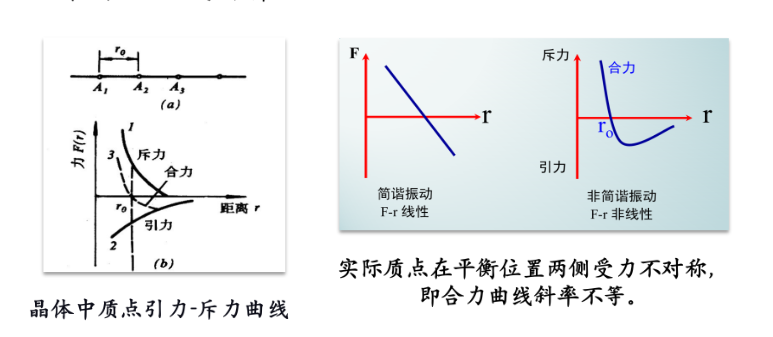
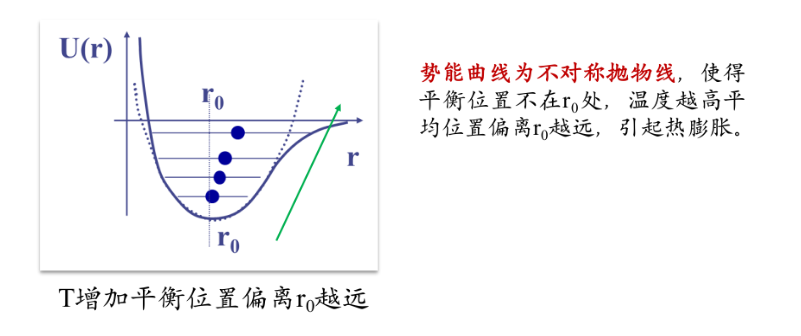
原子间结合力越强，膨胀系数越小

温度越低，热膨胀系数越小

与结构的关系：

1. 结构紧密程度：结构紧密的晶体（如石英）热膨胀系数大于结构疏松的无定形材料（如石英玻璃，），疏松结构的内部空隙可容纳部分膨胀体积。
2. 晶型转化：如氧化锆室温为单斜晶型，1300K以上转化为四方晶型，伴随4%体积收缩，导致热膨胀系数变化。
3. 各向异性晶体：弹性模量较高的方向膨胀系数较小，某一方向膨胀较大时可能迫使其他方向收缩，甚至出现负膨胀系数。
4. 晶体缺陷：晶体中的空位（辐照或淬火产生）会使膨胀系数增高
5. 多晶体和复合材料：
   • 工作温度下，多晶氧化钛膨胀系数低于单晶
   • 高温时趋于一致

冷却时晶粒热膨胀差异产生内应力，导致微裂纹和测试滞后；

复合材料若含易晶型转变组分，会因体积不均匀变化使热膨胀系数不均匀。

热传导

固体导热机理

• 气体 质点碰撞
• 金属 自由电子为主
• 非金属固体 晶格振动为主

声子导热

温度不是非常高时，光频支的能量较弱，导热以声频支为主。

固体内平均声子数密度满足：
$$n_{qs}=\frac{1}{\exp{(\frac{\hbar\omega_{qs}}{k_BT})}-1}$$
由温度决定。高温区声子数密度高，向低温区扩散，形成热流。

将晶格导热视为声子气体的扩散

气体热传导公式
$$\lambda=\frac{1}{3}C\nu l$$
固体（声子）热传导
$$\lambda=\frac{1}{3}\int C(\nu) \nu l(\nu)\mathrm{d}\nu$$
$\nu$为声子平均速度，C为声子体积热容，l为声子平均自由程

声子平均自由程受到声子间碰撞和杂质散射的影响

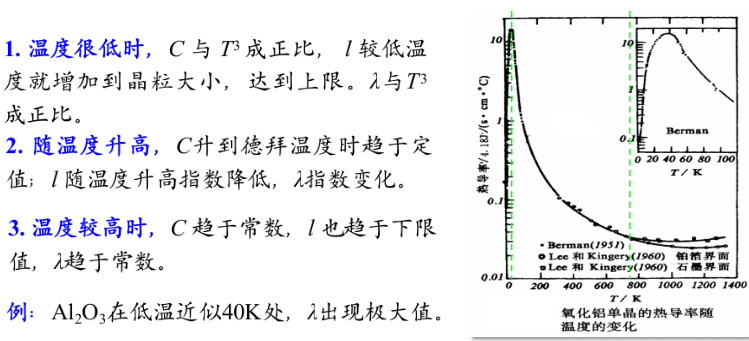
1. 声子碰撞

高温下平均声子数增大，自由程减小。热导率正比于$\frac{1}{T}$

低温下（小于德拜温度）散射减弱，热导率主要取决于自由程$l\to e^{\frac{\Theta_D}{T}}$
随温度降低指数上升。

温度继续降低到远小于德拜温度，声子平均自由程达到了晶粒尺寸，无法继续增加，变为常数。热导率此时主要取决于热容，以$T^3$降低。

2. 杂质和缺陷散射声子降低热导率

光子导热

光子导热依然与声子气体导热有相似形式

$$\lambda_r=\frac{1}{3}C_R\nu_rl_r$$
介质中$\nu_r=\frac{\nu}{n}$,n为折射率

透明材料中光子自由程大，辐射传热较为明显。单晶或玻璃对红外线较为透明，700K作用即有明显的辐射传热，而多数烧结陶瓷对辐射传热性能很差。

热导的影响因素

1. 温度

2. 显微结构
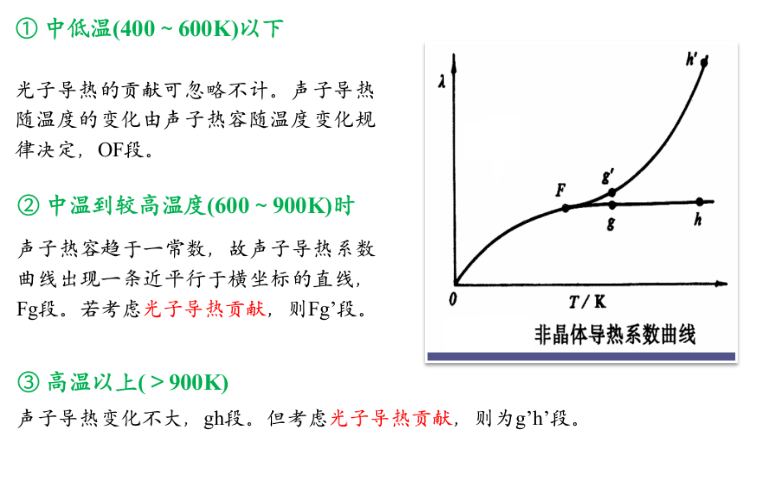
   • 晶体结构越复杂，散射越强，热导越低
   • 缺陷越多，热导越低
     温度升高，各向异性晶体趋于对称，不同方向差异减小
     3.多晶的热导总是低于单晶
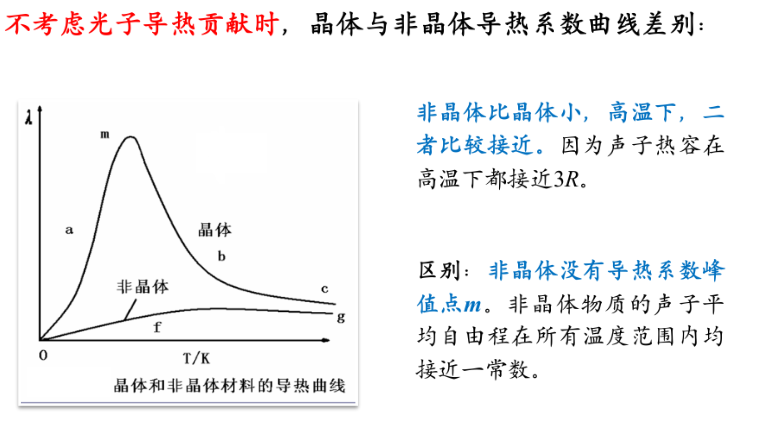
     4.非晶的声子自由程几乎为常数，热导率主要取决于热容

3. 化学组成
   原子质量越小，密度越小，热导率越大

4. 气孔

气孔使得热导率下降

玻璃体的热导率碎温度升高而增大，高于773K时，辐射传热使得热传导有较快上升$\lambda=cR+d$

某些建筑材料、耐火砖等有$\lambda=\lambda_{273K}(1+bT)$

热稳定性

热稳定性指材料承受温度剧烈变化而不失效的能力。

抗热冲击断裂因子

温度变化导致热膨胀，材料内部产生应力，应力集中使得材料失效。

骤冷临界温差
$$T_{max}=S\times \frac{\sigma_f(1-\mu)}{Ea}$$
S为形状因子、$\mu$为泊松比

第一热应力断裂抵抗因子R

$$R=\frac{\sigma_f(1-\mu)}{Ea}$$

第二热应力断裂抵抗因子R’

实际体系还存在散热

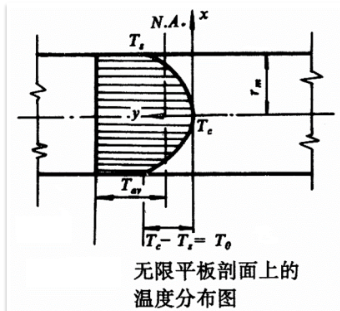
引入h为表面散热系数，对于半厚为$r_m$,热导$\lambda$材料，定义毕奥模数：
$$\beta=\frac{hr_m}{\lambda}$$
$\beta$越大冷却越快，对热稳定越不利。（约等于20视为骤冷）

实际应力不会达到理想骤冷的最大应力，实测的无因次表面应力$\sigma^*=\sigma/\sigma_{max}$

定义第二热应力断裂抵抗因子
$$R’=\frac{\lambda\sigma_f(1-\mu)}{Ea}$$
即为$\lambda\cdot R$

第三热应力断裂抵抗因子R’’

考虑实际体系允许的最大冷却速率。

导温系数表征了温度变化时材料内部温度趋于均匀的能力
$$\frac{\lambda}{\rho C_P}$$
定义第三热应力断裂抵抗因子
$$R’’=\frac{\lambda}{\rho C_P}\times \frac{\sigma_f(1-\mu)}{Ea}$$

材料能承受的最大降温速率

$$-(\frac{\mathrm{d}T}{\mathrm{d}t})_max=R’’\times\frac{3}{r_m^2}$$
冷却速率超过此值炸裂。

这些适用于均匀的脆性材料，气孔或者塑性相会钉扎热冲击微裂纹

抗热应力损伤因子

R’’’

$$R’’’=\frac{E}{\sigma^2(1-\mu)}$$
即为应变能释放率倒数。比较断裂表面能相同的材料。

R’’’’

$$R’’’’=\frac{2E\gamma_{eff}}{1-\mu}$$
$\gamma_{eff}$为断裂表面能，比较断裂表面能不同的材料。

提高抗热冲击断裂性能措施

核心判据公式

$$
R = \frac{\sigma_f(1-\mu)}{\alpha E}
$$
$$
R’ = \frac{\lambda\sigma_f(1-\mu)}{E\alpha}
$$
$$
R’’ = \frac{\sigma_f(1-\mu)}{E\alpha} \cdot \frac{\lambda}{\rho C_p}
$$

针对密实性材料的提高措施

1. 提高强度、减小弹性模量
   提升$\sigma_f/E$比值，增强材料韧性，使其在热冲击中吸收更多弹性应变能以避免开裂。金属材料的$\sigma_f/E$通常大于无机材料，因此抗热性能更优。
2. 提高热导率$\lambda$
   提升$R’$，使温差更快缓解、达到平衡。
3. 减小热膨胀系数$\alpha$
   材料在相同温差下产生的热应力更小。
4. 减小表面热传递系数$h$
   降低表面散热速率，例如在烧制冷却阶段维持炉内缓慢降温，可提升产品质量。
5. 减小产品有效厚度$r_m$
   可提升升降温速率。

针对多孔/粗粒/干压/部分烧制品的措施

以上措施仅针对密实性材料；对于多孔、粗粒、干压和部分烧制品，需从抗热冲击损伤角度考虑。

相关判据公式

$$
R’’’ = \frac{E}{\sigma^2(1-\mu)}
$$
$$
R’’’’ = \frac{2E\gamma_{eff}}{\sigma^2(1-\mu)}
$$

优化方向

• 减小弹性应变能释放率$G$和应力$\sigma$
• 增加弹性模量$E$和断裂表面能$\gamma_{eff}$

热功能材料

热功能材料主要包括形状记忆材料和梯度功能材料两大类

一、形状记忆材料

1. 定义：变形后经加热等处理可恢复初始形状，分为合金、聚合物、陶瓷三类。
2. 各类核心特点与应用：
   • 形状记忆合金：基于热弹性马氏体可逆相变，抗拉/疲劳强度高、耐蚀、生物相容性好（部分成本高），应用于机械紧固件（管接头、铆钉）、医疗器材（接骨板、支架）、航天天线等。
   • 形状记忆聚合物：含固定相（稳定）和可逆相（温敏转变），密度小、变形量大、成本低，应用于医疗固定、汽车缓冲、产品包装、火灾报警器等。
   • 形状记忆陶瓷：基于马氏体相变（如ZrO₂晶型转变），加热可恢复变形，适用于特定结构件。

二、梯度功能材料

1. 定义：组分、结构和性能呈连续梯度变化，无明显界面，可缓和热应力。
2. 核心特点：与传统复合材料相比，以特殊功能为设计目标，组织非均质连续变化，兼具不同材料优势（如陶瓷耐热+金属高强度）。
3. 应用：航天（耐1700℃的ZrO₂/Ni材料用于高速航天器）、汽车（活塞头热防护涂层）、核反应（内壁材料）、能源（燃料电池结构）、电子（压电陶瓷器件优化）等领域。